El relieve
terrestre se representa espacialmente mediante técnicas topográficas, las cuales junto
al desarrollo tecnológico han permitido la extensión de los llamados Modelos
Digitales del Terreno o MDT´s. Se denomina Modelo
Digital del Terreno a la representación numérica de la elevación de un territorio
en un medio digital. A partir de un MDT se pueden extraer las
siguientes variables del relieve terrestre: Altitud, Pendiente, Orientación y Curvatura o
Rugosidad. La
combinación física de estas variables da lugar a las formas del relieve, objeto
de estudio de la Geomorfología. Por lo que cada forma del relieve se materializa
con un algoritmo espacial de la combinación de las variables anteriormente
mencionadas.
 | |||
| Modelo Digital del Terreno |
Para crear
un MDT es necesario contar con información altimétrica de la superficie terrestre.
La manera más típica de representar esta información es a través de las
curvas de nivel. El principal procedimiento
para generar un MDT se basa en la triangulación entre vértices de las curvas de
nivel colindantes. Este método se conoce con el nombre de Red Irregular de Triángulos o
Triangle Irregular Network (TIN). Los TIN se sustentan en la condición de
Delaunay, la
cual dice que la circunferencia circunscrita de cada triángulo de la red no debe
contener ningún vértice de otro triángulo.
 |
| Triangulación de Delaunay |
Esta
triangulación está relacionada con los polígonos de Thiessen o
Diagramas de Voronoi. Estos polígonos delimitan áreas de proximidad a los
diferentes puntos. En otras palabras los diagramas de Voronoi se crean a partir
de una interpolación basada en la distancia euclidiana que nos informa sobre
cuál es el punto más cercano en cada lugar del espacio estudiado. La relación
con la condición de Delaunay consiste en que los centroides de cada
circunferencia circunscrita conectados dan lugar a los polígonos de
Thiessen.
 | |
| Diagrama de Voronoi |
Las
tecnologías de la información geográfica ponen en manos de analistas del territorio una herramienta capaz de calcular infinidad de
algoritmos necesarios para realizar los modelos digitales del relieve terrestre.
A partir de estos modelos se pueden analizar multitud de relaciones espaciales y
caracterizar el territorio de manera más precisa, lo que redunda en una mejor
planificación y gestión territorial.
Tener
modelizado el relieve terrestre permite posteriores aplicaciones que dan lugar a
estudios específicos. Algunos estudios derivados de los MDT´s son el cálculo de
las zonas de sombra según la altura y el azimut del sol, las zonas visibles
desde un punto de observación, la radiación solar que llega a la superficie
terrestre o el cálculo de la dirección y la acumulación potencial de un flujo a
lo largo del relieve.
Información requerida
Para
realizar un MDT y sus posteriores explotaciones es necesario poseer información
altimétrica de la superficie terrestre. Para el ejercicio que se expondrá a
continuación se usarán las curvas de nivel para El Municipio de Santiago de Cali. Además para extraer el MDT con la forma exacta de la isla será necesario tener
una capa de polígonos con un único polígono que delimitará el perímetro municipal.
 | |
| Curvas de Nivel del Municipio de Cali |
Procedimiento técnico
1. Crear un MDT a Partir de Curvas de Nivel: Para ello debemos utilizar la extensión 3D Analyst de ArcGis, desplegar la función TIN Management y ejecutar Create TIN.
 |
| Modelo de Red Irregular de Triángulos |
2. Obtener un Raster de altitud a partir del TIN: A continuación debemos ejecutar la herramienta de conversión TIN to Raster para obtener el modelo de alturas.
 |
| Modelo raster de altitud |
El resultado es un modelo en el cual cada pixel contiene
los valores X,Y y Z en dicho punto. en este caso se genero un raster con
celdas cuadradas de 111m * 111m, basados en el nivel de detalle de la
información topográfica
3. Obtener un raster de pendientes a partir del raster de altitud: Debemos ejecutar la herramienta Slope de la extensión Spatial Analyst de ArcGis (dentro
de Surface). Se puede seleccionar la opción Degree para obtener la
pendiente en grados o Percent para obtenerla en porcentajes.
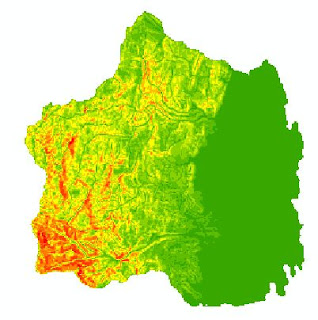 |
| Modelo de pendientes de Cali |
La pendiente es una variable geométrica
continúa, obtenida a partir del MDE; es definida como el ángulo formado por la
superficie del terreno y la horizontal. Se expresa en grados, en un rango entre
0 y 90. los colores rojos indican pendientes fuertes, mientras que los colores verdes indican pendientes suaves
4. Obtener un raster de orientacion a partir del raster de altitud: A continuación ejecutamos la herramienta Aspect dentro Spatial Analyst / Surface.
 |
| Modelo de orientación de ladera |
La orientación es definida como la dirección de exposición de la ladera en un punto y que
representa la dirección de la máxima pendiente calculada para cada celda. Se calcula a partir del ángulo existente
entre el norte geográfico y la proyección sobre el plano horizontal del vector
normal a la superficie en un punto dado. La orientación indica de manera indirecta la situación de una ladera
en cuanto a su insolación y, por lo tanto, si una ladera se encuentra húmeda o
seca con mayor frecuencia
5. Obtener un raster de Luminosidad (Hillshade) a partir del raster de altitud: Debemos ejecutar la herramienta Hillshade dentro de Spatial Analyst / Surface
 |
| Modelo de Sombras de Cali |
El resultado es un
mapa que representa el relieve hipotético de una región geográfica bajo
estudio si estuviera expuesta a una fuente de luz proyectada hacia
ella con determinado azimuth (dirección angular del sol, en donde 0° es el este,
90° el norte, 180° el oeste y 270° el sur) y altitud (pendiente de inclinación
sobre la horizontal de la fuente de luz). para una mejor representación se recomienda remuestrear el hillshade durante su visualización a travéz del método de interpolación bilineal o convolución cúbica debido a que producen sobre la imagen cierto suavizado en la textura
5. Obtener un raster de Visibilidad de la zona de estudio a partir del raster de altitud:
 |
| Modelo de visibilidad |
Este tipo de mapas permiten determinar que porciones de un territorio se pueden observar en todas las direcciones desde algún (nos) punto (s) de observación (s) determinado dentro del mismo. Para su creación es necesario definir los datos de entrada y el o los puntos de vista. en verde aparecen las porciones del territorio que son visibles, mientras que en rojo aparecen las porciones del mismo que no son visibles desde el punto de observación.
Interpretación de resultados
Los
productos derivados de los Modelos Digitales del Terreno permiten un
acercamiento mucho más preciso espacialmente a las características físicas del
relieve terrestre. La pendiente, orientación, altitud, …de cada punto del
territorio, al estar modelizadas, permiten a los Sistemas de Información
Geográficas, por ejemplo, aplicar ecuaciones hidrológicas de los comportamientos
del agua sobre el relieve. Todo esto desde un punto de visto atemporal.
La
incorporación de la variable tiempo es una de las ramas donde los SIG están
centrando sus evoluciones más recientes. Imaginemos las posibilidades que
tendrían los SIG si estos modelos espaciales del relieve permitieran avanzar o
retroceder en el tiempo aplicando unas condiciones ambientales estándares. Esto
daría lugar a unos procesos geomorfológicos específicos, los cuales serían
sistematizados en algoritmos que se aplicarían al modelo digital del terreno. El
resultado sería el relieve pasado o futuro en cada lugar del
territorio.
En suma, con este tipo de análisis es posible determinar una representación gráfica
adecuada de los datos para su interpretación y toma de decisiones.
Espere
próximamente la segunda parte de esta entrada del blog donde aprenderemos cómo calcular el volumen de un barranco.
descargue en PDF e imprima la primera parte a continuación: utilice las herramientas, zoom, vista en pantalla completa, descargar, imprimir
Si esta entrada te ha gustado compartela
No hay comentarios:
Publicar un comentario